Variational Auto Encoder와 ELBO(Evidence Lower Bound)

* 이 글은 현재 참여하고 있는 스터디 모임에서 발표한 내용으로, 여기에 직접 게시한 글을 옮겨 수정하면서 등록하였습니다.

 

Auto-Encoding Variational Bayes, 2014  pdf

비록 나온지 오래된 논문이지만 딥러닝 영역에서 막대한 영향을 끼친 VAE에 대해서 간단한 개념과 함께 사용된 목적함수가 갖는 의미에 대해서 설명해 보고자 한다. 

 

Auto Encoder

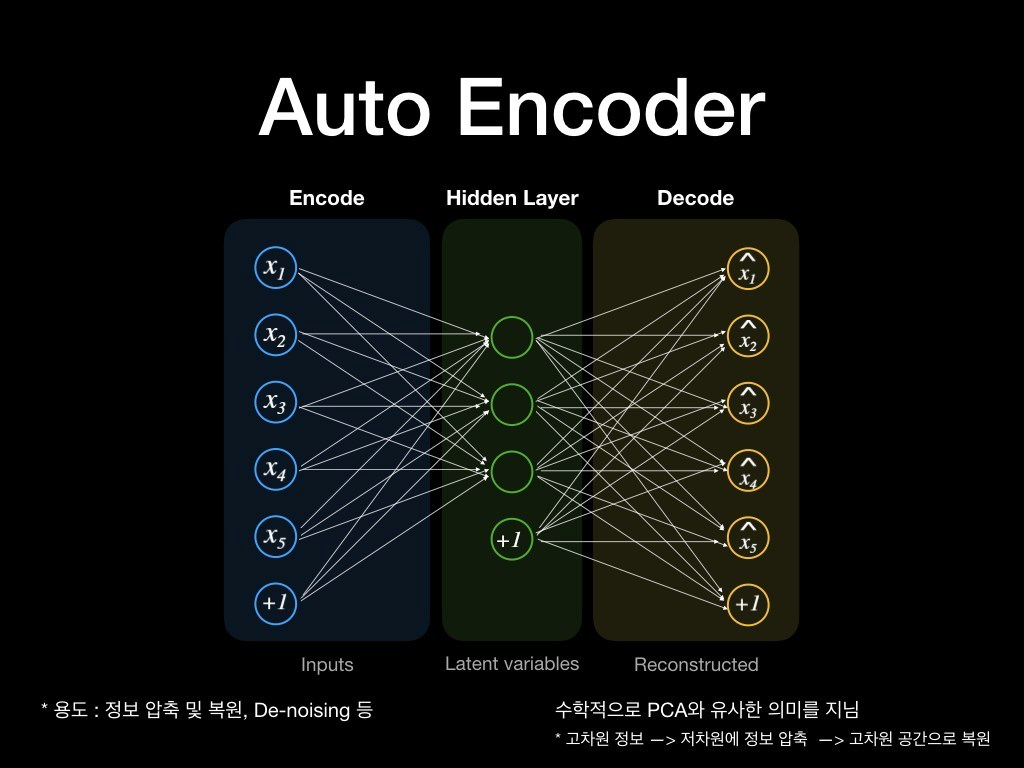
 오토인코더(Auto Encoder)는 위 그림과 같이 크게 인코더(Encoder)와 디코더(Decoder) 두 파트로 구성된다. 어떤 입력에 대해 특징을 추출하여 압축된 정보를 잠재 변수(Latent variables)에 담고, 잠재 변수로부터 자기 자신(입력)을 복원해 내는 알고리즘이라 볼 수 있다.

 인코더를 통해서 정보를 압축하거나 디코덜ㄹ 통해 정보를 복원하는 등의 역할을 수행할 수 있으며, 의미있는 특징을 추출하거나 정보를 압축하는데 사용되는 PCA와 수학적으로 유사한 의미를 지니게 된다. 또한 노이즈가 입력에 대해서 denosing 하는 문제 영역에서도 효과적으로 활용될 수 있다.

 

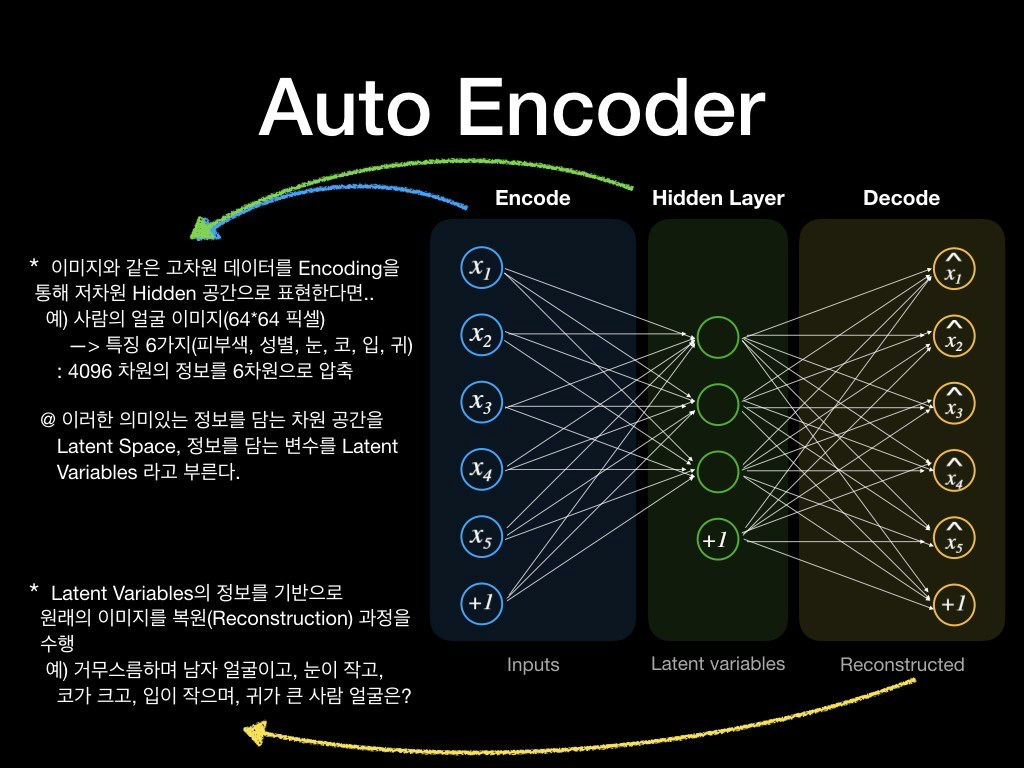
 오토인코더에 대해 조금 더 들여다 보도록 하자. 

 예를 들어 64*64 크기의 얼굴 이미지가 있다고 할 때, 4096차원의 입력 영상은 인코더를 통해 저차원의 Hidden 공간으로 압축된다. 히든 공간이 6차원 벡터로 표현된다고 할 때, 편의상 "피부색, 성별, 눈, 코, 입, 귀"라는 6가지 특징으로 표현되었다고 가정하자.

  (의미있는 정보로 압축된 Hidden 공간을 Latent Space, 이 변수들을 Latent Variables라 한다)

 

 디코더의 역할은 입력된 얼굴로 표현된 피부색, 성별, 눈, 코, 입, 귀 정보에 해당하는 특징 벡터만을 가지고 새로운 얼굴 이미지를 생성하게 된다. 얼굴이 검고, 남자이며, 눈이 작고, 코가 크고, 입이 작으며, 귀가 큰 사람의 얼굴을 상상한다고 보면 되겠다.

 

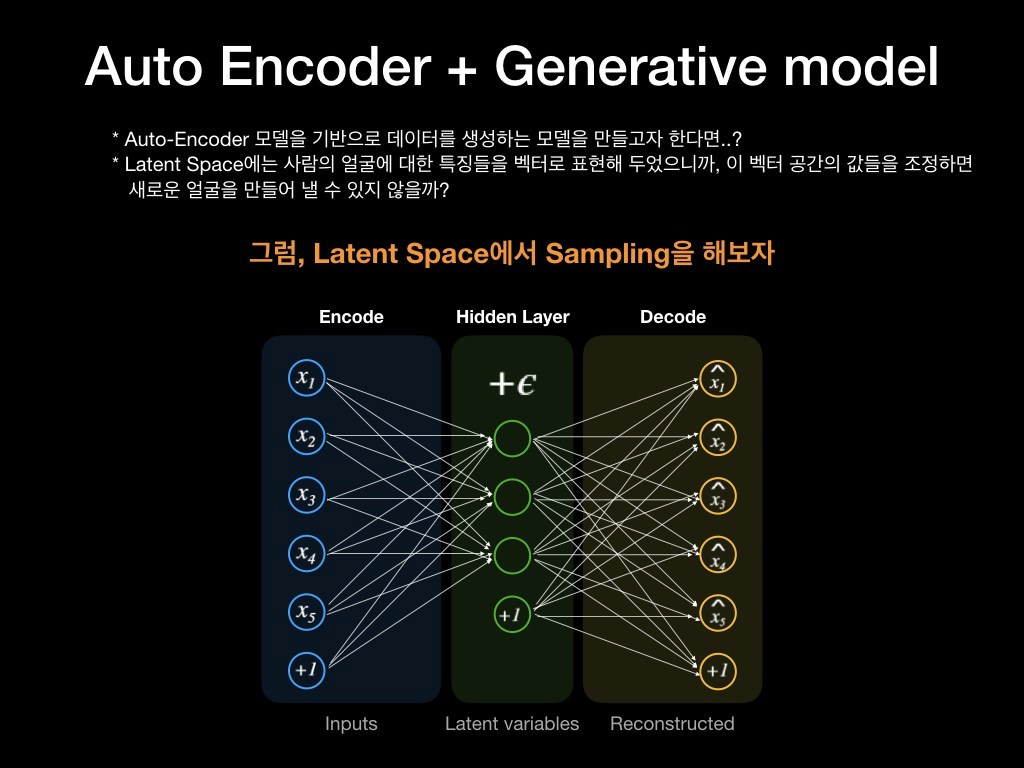
 다시 말해 Latent Space는 입력 데이터들에 대한 특징벡터로 이루어진 공간으로써, 정보를 함축하고 있다. 그렇다면 "Latent Space로부터 데이터를 생성해 낼 수는 없을까?"라는 생각을 할 수도 있을 것이다.

 

Variational Auto Encoder

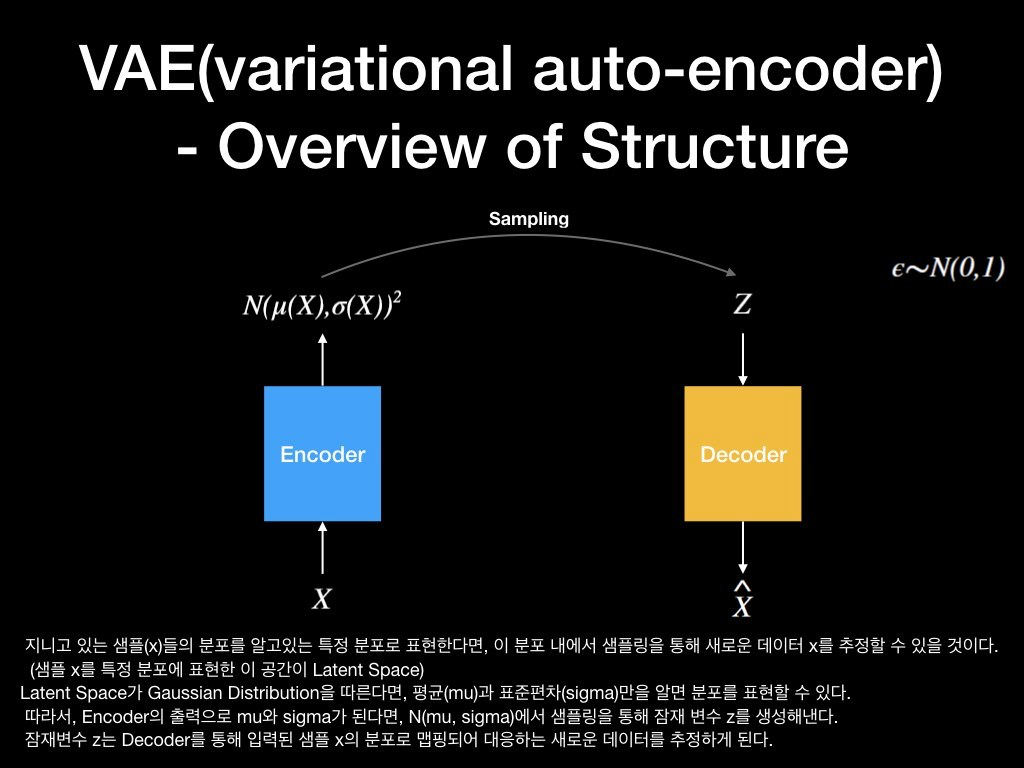
 내가 가지고 있는 데이터(X)들은 너무 많고 고차원이기 때문에, 새로운 데이터를 만들어 내기가 어렵다. 만약 샘플(X)들의 분포가 사전에 알고있는 어떤 분포(예를 들어 정규분포)로 표현할 수 있다면, 알고 있는 분포로부터 샘플링을 통해 새로운 데이터 X'를 추정해 낼 수 있을 것이다. (실제 데이터의 분포와 알고있는 어떤 분포를 Mapping)

 

 만약 오토인코더의 잠재 공간이 우리가 잘 아는 정규분포를 따른다고 할 때, 이 분포는 평균(mu)과 표준편차(sigma)로 표현될 수 있을 것이다. 따라서 인코더의 출력이 mu과 sigma가 된다면, 정규분포 N(mu, sigma)에서 샘플링을 통해 잠재 변수 z를 생성할 수 있고, 생성된 잠재변수 z는 디코더를 통해 입력된 샘플 X의 분포로 맵핑되어 대응하는 새로운 데이터를 추정할 수 있게 된다.

 그런데 샘플링을 하게 되면 Random성을 띄기 때문에 인코더와 디코더가 Random하게 연결되게 되고, 이는 미분이 불가하기 때문에 모델 학습이 불가하게 된다. 이를 해결하기 위해 아래 그림에 보인 Reparametrization trick을 적용한다.

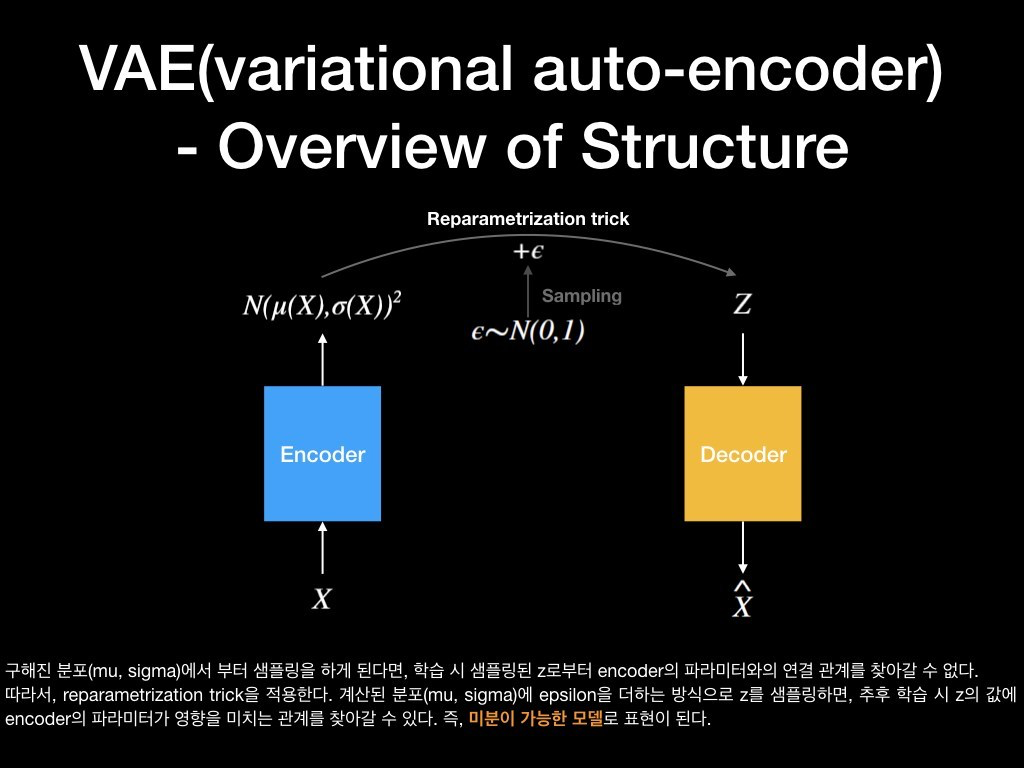
 논문에서는 Reparametrization Trick이라 불리는 트릭을 통해 N(mu, sigma) + e, e~N(0, 1) 와 같이 e를 출력에 더해주는 형태를 취함으로써, 인코더가 잠재 변수 z에 미치는 영향 관계를 찾을 수 있게 된다. 즉, 미분이 가능한 모델로 표현이 가능해진다.

 

KL Divergence

 VAE의 목적함수를 설명하기 앞서, KL Divergence에 대해 짚고 넘어가자.

 

 Divergence란 두 확률 분포의 다름의 정도를 나타내는 것이다. KL Divergence(이하 KLD)는 Divergence의 많은 방법 중 한가지 방법으로 아래 그림의 식과 같다.

이때 KLD의 주요 성질/특징은 다음과 같으며, 이 성질/특징을 잘 기억하도록 하자.

 1) KLD는 항상 0 이상의 값을 지닌다.  : 두 분포가 같을 때에는 0, 분포가 다를 수록 값이 커짐

 2) 계산의 순서가 바뀌면 값이 변할 수 있다.

 3) 두 분포가 정규분포를 따를 때 간략하게 표현이 가능함.

 3번 성질의 경우 직접 두 정규분포 식을 KLD 식에 대입하여 전개를 해보면 아래와 같이 간단하게 표현된다.

 

베이즈 정리 (Bayes Rule)

 베이즈 정리도 VAE의 목적함수를 해석하는데 매우 중요한 역할을 하니 기억해야 한다.

(베이즈 정리에 대한 자세한 내용은 향후에 공부해서 별도 포스팅을 하고, 여기에서는 간단하게 넘어간다.)

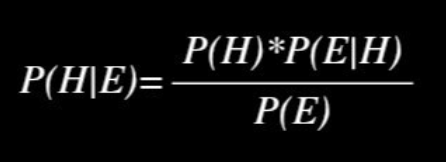
E : Evidence

H : Hypothesis

 

P(H) : Prior Probability - 사전에 알고있는 H가 발생할 사전 확률
P(E|H) : Likelihood of the evidence 'E' if the Hypothesis 'H' is true - 모든 사건 'H'에 대하여 E가 발생할 우도

         -> How well H explains E : 각 H가 E를 얼마나 잘 나타내는가.

P(E) : Prior probability that the evidence itself is true - 'E'에 대한 사전 확률. E가 발생할 확률

P(H|E) : Posterior Probability of 'H' given the evidence - E가 주어졌을 때, H가 발생할 사후 확률

         -> "주어진 현 사건(E)에 대해서 H가 발생할 믿음" 정도로 해석

 

몬테카를로 방법/근사 (Monte Carlo Approximation)

 

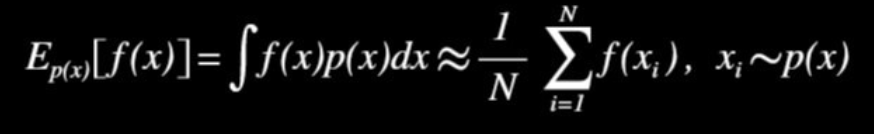
다만, 이 식은 "확률 밀도 함수 p(x)를 따르는 x에 대한 f(x)의 기대값은 p(x)를 따르는 샘플들로 근사할 수 있다"라고 이해할 수 있다.

(몬테카를로 방법에 대해서도 자세한 내용은 향후에 공부해서 별도 포스팅 하겠다.)

 

목적함수 : ELBO(Evidence Lower Bound)

VAE는 AE에 Generative Model을 적용하고자 하는 것이 목적이고, 이때 우리는 주어진 샘플 X에 대한 복잡한 분포를 알 수 없기 때문에 이를 잘 알고 있는 정규 분포로 나타내고, 이 정규 분포로부터 다시 주어진 샘플 X의 분포를 따르는 샘플을 생성해내는 것이다.

step 1.

 이를 위해서 "주어진 샘플 X의 확률 분포를 잘 표현해보자"를 식으로 나타내기 위해 잠재 변수 z의 분포를 이용하여 아래와 나타낼 수 있다.

  1) 베이즈 정리의 조건부 확률 식을 이용하여, 샘플 x가 발생할 확률(P(X))을 치환하고, 이때 (알고있는) 잠재변수 z의 분포를 이용한다.

  2) Log를 취함으로써, Multiply Term을 분해한다.

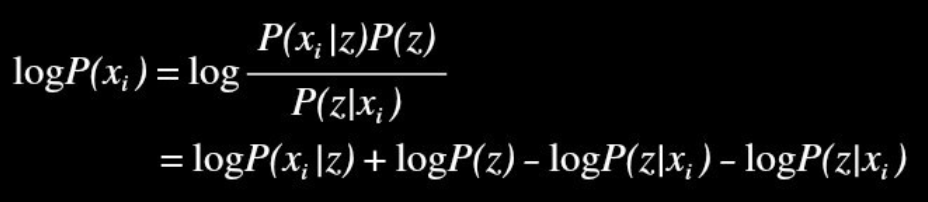
step 2.

 위 식과 같은 목적이며, 확률 분포를 따르는 잠재변수 z의 확률 밀도함수의 성질을 이용하여 아래와 같이 식을 변형한다.

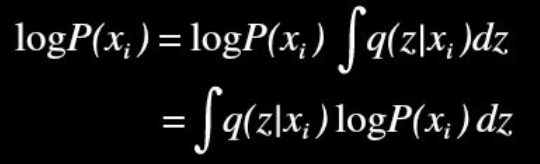
P(x)에 적분 텀이 추가된 것은 모든 샘플 x_i에 대한 샘플 z가 생성될 확률 밀도함수를 적분하면 아래와 같이 1이 되기 때문에, P(x)의 식에 다시 자기 자신을 포함하는 재귀 형태로 식이 표현될 수 있다.

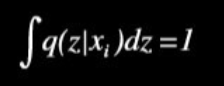
step 3.

 step 1의 식을 step 2에 대입하면, 노란색 부분은 몬테카를로 방법에 의해 기대값으로 근사하여 표현가능하다. 그리고 초록색 밑줄 부분과 같이 Term을 +-하여 식의 등식이 유지되게 한다.

 이렇게 되면, 앞에서 언급하였던 KL Divergence의 식이 2개나 나타나게 된다(파란색 밑줄, 빨간색 밑줄).

 파란색 밑줄 부분은 잠재변수 z가 알고있는 확률 분포(정규분포)를 따르기 때문에 KLD의 계산이 쉽다. 하지만, 빨간색 밑줄 부분은 가지고 있는 샘플 X의 복잡한 분포를 실제로 알지 못하기 때문에 P(z|x_i)를 계산할 수 없다.

 이때, KLD는 항상 0 이상의 값을 갖는다는 특성이 있으므로, 마지막 식과 같이 등호를 부등호로 나타낼 수 있게 된다. 즉, 이는 X의 확률 분포를 잘 표현해보자는 목적함수의 하한 경계를 나타낸다.

step 4

 "가지고 있는 데이터 X의 분포를 잘 표현해보자" 라는 목적으로 위 노란색 박스와 같은 식에 도달하였다. 결국 분포를 잘 표현해보자 라는 목적에 부합하기 위해 log P(x)가 최대가 되는 방향으로 모델을 학습하면 된다.

 

 KLD 부분의 식의 구현은 q(z | x_i)가 주어진 샘플 x_i에 대해 인코더를 통과해 얻어진 mu와 sigma를 따르는 정규분포가 될 것이며, P(z)는 z~N(0, 1)를 만족한다고 할 때, 모두 정규분포이므로 간단하게 표현할 수 있다.

 

 파란색 밑줄 Reconstruction Error에 해당하는 Term을 해석하면, 샘플 x가 주어졌을 때 z가 인코더의 결과로 얻어진 분포를 따르고, 이때 다시 z일때 샘플 x가 생성될 확률의 기대값... 복잡하다.

 결국 입력 데이터가 인코더를 통해 정규분포를 따르는 어떤 공간에 표현되었고, 이로부터 다시 디코더를 통과해서 생성된 x'가 x가 되게끔 하는 것을 목적으로 하는 것이다. 그렇기에 이 Term은 Reconstruction Error을 의미하게 된다.

 따라서, x가 나타날 확률을 계산하는 것은 가지고 있는 샘플들에 대한 확률 분포를 찾고자 하는 것이므로, z로부터 x가 나타날 확률을 최대화 하는 것이므로 MLE(최우 추정법)이 되며, 이는 다시 Cross Entropy로 표현된다.

 

실험 결과

 얼굴 이미지와 숫자 이미지에 대한 VAE 학습 결과이다. 모두  Latent Space 공간을 2차원 정규분포로 표현한 것이고, 위 이미지의 중심을 원점으로 정규분포가 생성되어 있다고 할 때, 그 분포를 기반으로 샘플링된 z를 기반으로 생성된 x 데이터를 표현한 것이다.

 얼굴 이미지의 경우 표정과 얼굴의 방향 등이 인접한 사진끼리는 유사하고, 멀리 떨어질 수록 특성이 달라짐을 볼 수 있다. 숫자 이미지 또한 가까이 있는 이미지끼리는 유사하고 멀리 떨어질수록 특성이 달라짐을 볼 수 있다.

 

 이렇듯 주어진 데이터들의 복잡한 분포를 정규분포와 같이 알고있는 분포와의 관계를 찾았기 때문에, 알고있는 분포로부터 샘플링을 통해 실제 데이터와 같은 데이터를 생성해낼 수 있다.

 

 

고찰

 많은 문제 영역에서 AE / VAE 등을 응용한 방법이 많이 등장하고 있고, 또한 이 포스트에서 다룬 KLD나 베이즈 정리, 몬테카를로 방법 등도 수많은 논문과 연구에서 이용되고 있다. 실제 문제에 적용하는 데 있어, 공개된 코드들도 많고 Pretrained 모델도 많이 있기 때문에 사실 위 내용들을 자세히 들여다 보지 않아도 될 것이다. 하지만 그냥 그렇구나 하고 볼때와 의미를 해석하고 볼때 느껴지는 것은 매우 다를 것이다. 이를 느낌으로써 보이는 시각 또한 달라 질 것이라 생각한다.

 

 작년에 작성한 포스팅 글을 그대로 가져오면서 공부하고자 다시 따라 쓰면서 조금씩 수정하였습니다. 잘못된 부분이 있거나 의견/질문이 있으시면 문의주세요.